
For a full list of BASHing data blog posts, see the index page. ![]()
Two special data validations
The title of this blog post is a bit silly, because all data validations are special cases. For any data processing operation you can identify data "of the wrong sort" that you want to exclude from the process, but how do you define "right" and "wrong"? It depends!
Triangulation. Volunteers at an arboretum in my part of the world locate their newly planted trees by triangulation. They record the distances (to the nearest 0.1 m) to a tree base from each of two nearby in-ground markers which have known coordinates (eastings and northings) — see the diagram below.
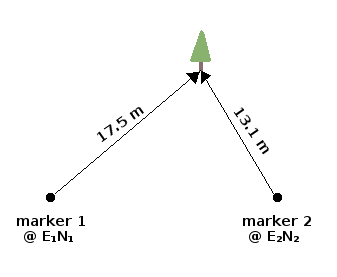
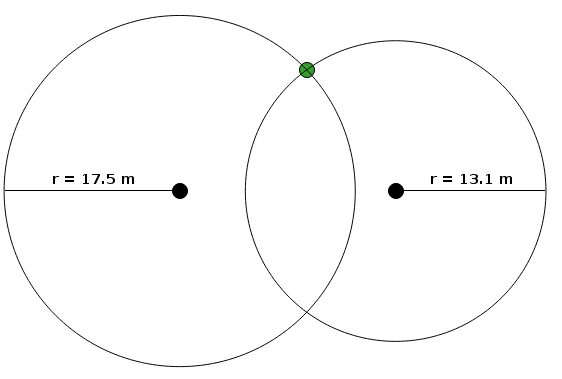
There are two simple ways to get the coordinates of the tree. The first is to buffer the two markers in a GIS program with circles whose radii are the measured distances. The circles will intersect at two points. The GIS user knows on which side of the inter-marker line the tree was planted, so the correct intersection is selected and its coordinates read off in the GIS window (or the intersection is added as a point feature in a "trees" layer ):
A second method is to calculate the locations of those two circle intersections using trigonometry, then select the correct intersection by inspection of the coordinates. I wrote a shell script to do this with YAD dialogs for user input and for reporting; the results are also logged to a "triangulations" text file. As one kind of validation, the script checks that the two marker strings entered are listed in a look-up table that has all the markers and their coordinates.
The script works well, except when it doesn't. One (or both) of the measured distances might be incorrect, or the wrong marker pegs might have been recorded. The result might be that the two circles don't intersect, as in this example:
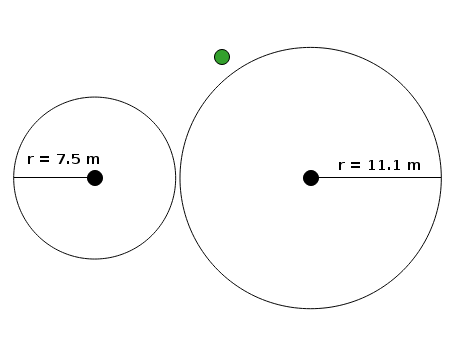
I added another validation test for this class of problem. If the input data fail the test, a YAD dialog reports "The two circles don't intersect".
The test is based on a fundamental property of triangles, sometimes called the triangle inequality. If the input data are correct, then the tree and the marker pegs form a triangle in which the sum of the lengths of any two sides is greater than or equal to the length of the remaining side. If this isn't true for the input data, then the data don't describe a triangle.
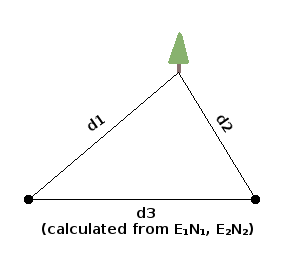
In a shell script where the distance variables are d1, d2 and d3, the test is:
if (( $(echo "$d1 > ($d2+$d3)" | bc) )) || (( $(echo "$d2 > ($d1+$d3)" | bc) )) || (( $(echo "$d3 > ($d1+$d2)" | bc) ))...
These BASH arithmetic constructs evaluate to TRUE or FALSE. bc is used here because BASH can only do integer arithmetic.
Regular records?
In a recent BASHing data post I showed one way to number "irregular" multi-line records. The file had some records with 2 lines, some with 3 and some with 4. If the file had been regular, as in the file "regs" with exactly 3 lines per record:
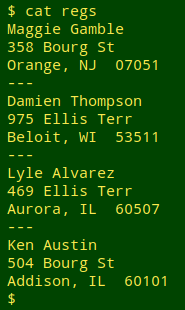
then the records could be numbered by counting lines, for example like this:
awk 'NR%4==1 {printf("%04d\n",++c)} 1' regs
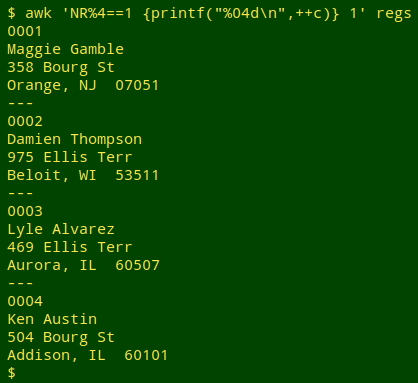
The final "1" tells AWK that every line is to be printed, but there's a special instruction for any line in which the line number gives a remainder of 1 when divided by 4 (NR%4==1). That condition selects lines 1, 5, 9 and 13, the lines with personal names. At those lines AWK printfs a pre-incremented count (++c ) of the lines, with the count padded with zeroes to the left to 4 places (%04d), followed by a newline.
In a big file, though, how could you be sure that all the records were regular? One way is to define a record as the bit between the "---" lines, and the fields within each record as the bits between newlines, and then count fields per record:

The last record (and only the last record) will have 4 fields because that record ends with a newline, but all other records should have 3 fields, in other words 3 lines. If I delete a line from a record, the validation detects the problem:
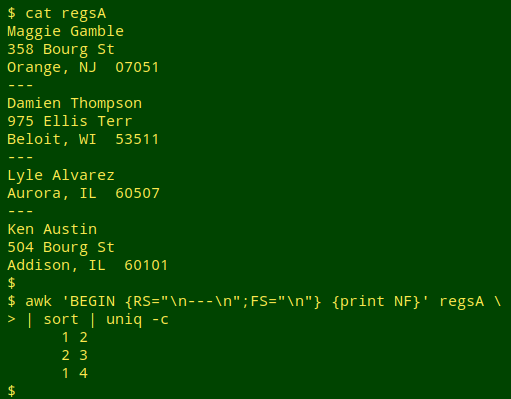
and the irregular record can be identified by its unusual field count:

Last update: 2019-03-03
The blog posts on this website are licensed under a
Creative Commons Attribution-NonCommercial 4.0 International License