---

For a full list of BASHing data blog posts see the index page.     

---

The curious world of check digits

In many standardised numerical codes, one or more digits are special. They're called check digits and they can be used to check that the code hasn't changed due to human or computer error.

For example, my Australian Business Number, or ABN, is 42 021 773 747. The last nine digits are my unique identifier and the first two digits are for checking. But the ABN check isn't simple:

• Subtract 1 from the first (left-most) digit of the ABN to give a new 11 digit number
• Multiply each of the digits in this new number by a "weighting factor" based on its position as shown in the table below
• Sum the resulting 11 products
• Divide the sum total by 89, noting the remainder
• If the remainder is zero the number is a valid ABN

Position | Weighting
1 | 10
2 | 1
3 | 3
4 | 5
5 | 7
6 | 9
7 | 11
8 | 13
9 | 15
10 | 17
11 | 19

Later in this post I demonstrate some ABN validating code, but meanwhile here are two more examples of check digits.

---

VISA credit card 16-digit numbers, 4nnn nnnn nnnn nnnN
 
The first digit (4) identifies the VISA network. Digits 7-15 are the card account number. The check digit (N) is calculated from the other 15 digits going from right to left. The first and every second right-to-left digit is doubled. Some of the doubles will be greater than 9, in which case the double is replaced by the sum of its digits, e.g. doubling a 6 gives you 12, which is reduced to 1+2 = 3. Add up the 15 digits after this operation and multiply the sum by 9. The check digit is the remainder after the product by 10.

This particular check digit procedure is based on the Luhn algorithm, and it's used with a wide range of numerical codes. Let's try it out with a VISA card from an advertisement:

Start with | Doubling | Reducing
6 | 12 | 3
8 | 8 | 8
7 | 14 | 5
6 | 6 | 6
4 | 8 | 8
2 | 2 | 2
1 | 2 | 2
4 | 4 | 4
3 | 6 | 6
2 | 2 | 2
1 | 2 | 2
4 | 4 | 4
3 | 6 | 6
2 | 2 | 2
4 | 8 | 8

 
Sum of last column's digits = 68
(9 x 68) = 612; mod 10 = 2
2 NOT equal to check digit 7, so card number is invalid!

---

International Standard Serial Number (ISSN), nnnn-nnnN
 
This is another last-digit-is-check-digit format. In this case each non-check digit is multiplied by its position number, where the positions are counted from right to left. The first number of the ISSN is at position 8, the second at position 7, and so on. The sum of the 7 products is then divided by 11. The remainder subtracted from 11 is the check digit and it can range from 0 to 10, but a check digit of "10" is represented with the Roman numeral "X".

For example, the Australian magazine with the biggest circulation is The Australian Women's Weekly and its ISSN is 0005-0458:

Start with | Position | Product
0 | 8 | 0
0 | 7 | 0
0 | 6 | 0
5 | 5 | 25
0 | 4 | 0
4 | 3 | 12
5 | 2 | 10

 
Sum of products = 47
47 divided by 11 has remainder 3
Subtract 3 from 11 to get the check digit, 8

---

Check digit algorithms vary in how well they can detect various error types, like digit replacements, digit swap-arounds within a number, digit insertions and digit deletions. Some algorithms are fairly complicated, but all of them are more or less easily code-able in your favourite programming language.

Here's my AWK code for an ABN validator (see top of this page), looking first at my own (valid) ABN, then a variant with one digit replaced:

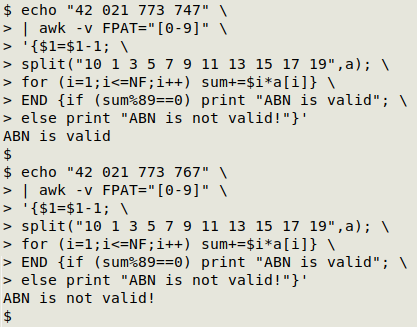
The 11-digit ABN number is fed to AWK by echo. Fields are defined with -v FPAT="[0-9]", which means that a field is any single digit. Thanks to this definition, it doesn't matter whether or not there are spaces in the ABN to be tested.
 
Next, the first field (first digit) is redefined to be one less than its starting value ($1=$1-1).
 
I then build an array "a" with the split function acting on the string of "weighting factor" values for the 11 digits. The array is indexed with character position. In other words, a[1]=10, a[2]=1, a[3]=3, a[4]=5 and so on: split("10 1 3 5 7 9 11 13 15 17 19",a).
 
Working through the 11 fields (digits) with a for loop (for (i=1;i<=NF;i++)), I multiply each digit (including the redefined first digit) by its weighting factor and add the product to the variable "sum" (sum+=$i*a[i]).
 
In the END statement, I check whether the remainder after dividing "sum" by 89 is zero (if (sum%89==0)). If it is, AWK prints "ABN is valid", otherwise "ABN is not valid!".

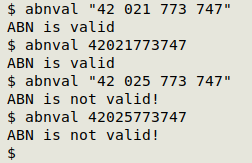
The code can go into a shell function, "abnval":

abnval() { echo "$1" | awk -v FPAT="[0-9]" '{$1=$1-1; split("10 1 3 5 7 9 11 13 15 17 19",a); for (i=1;i<=NF;i++) sum+=$i*a[i]} END {if (sum%89==0) print "ABN is valid"; else print "ABN is not valid!"}'; }

---

Last update: 2021-06-16
The blog posts on this website are licensed under a
Creative Commons Attribution-NonCommercial 4.0 International License

---