
For a full list of BASHing data blog posts see the index page. ![]()
A sunset surprise
Early in January my wife asked a head-scratcher of a question:
We're past the summer solstice (21 December 2020 here in Australia) so the days must be getting shorter. Then why isn't the sun setting earlier? It's getting dark at the same time every evening.
I dug into some sunrise/sunset data to find the answer. When I found it, I realised that it would be very hard to explain what was happening without pictures, which is why this post has data graphics instead of the usual terminal screenshots!
My data source was the excellent timeanddate.com website. I used the site to get sunrise and sunset times for our town in Tasmania, as well as solar noon times (more on that later). The data for December 2020 and January 2021 are shown below in the "clock" time curves:
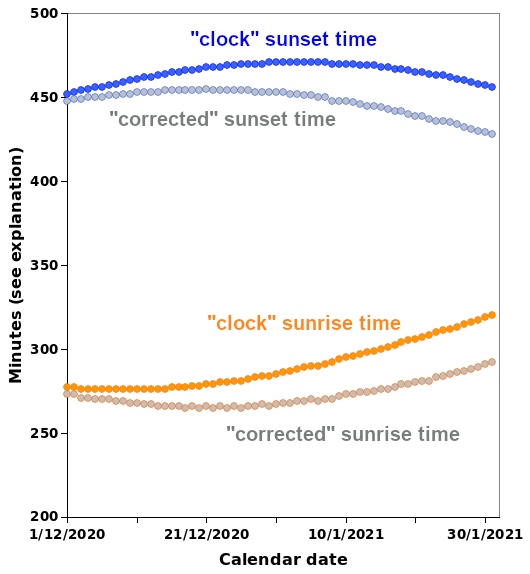
The Y-axis is in minutes before or after "clock" noon on the day shown, but for sunrise times (the before times) I've arbitrarily added 12 hours to bring the sunrise and sunset curves closer together. Times are Australian Eastern Standard.
So the days had indeed been getting shorter, and 5 January (for example) was almost 8 minutes shorter than 21 December, the longest day. But sunset on 5 January was 3 minutes later than on 21 December. As shown in the graphic above, sunrise on clock time was getting steadily later from mid-December, but sunset on clock time peaked broadly in early January, and was only getting noticeably earlier towards the end of the month.
On to the Equation of Time, shown in the second graphic:
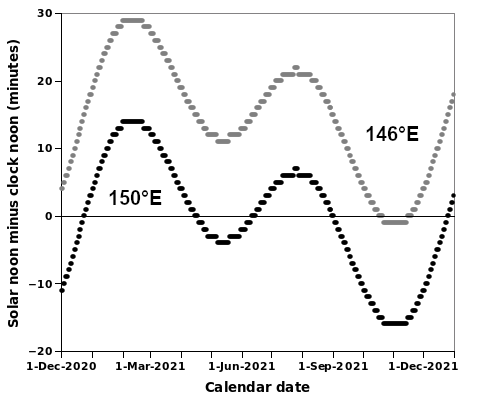
"Solar noon" is the time when the sun reaches the highest point on its path in the sky. You can think of that as midday, and also that it should be the same as "clock noon", or 12 pm. But it usually isn't. Solar noon can be earlier or later than 12 pm, depending on the time of year. This annual variation is shown above in the "150°E" curve, which is an Equation of Time graph. At the beginning of March, midday is about a quarter of an hour later than 12 pm. At the beginning of December, it's about a quarter of an hour earlier.
This "wobble" of solar noon around clock time has been known since ancient times, although it was many centuries before its causes were well understood. Wikipedia has an excellent article on the causes and calculation of the wobble. The "Equation" in Equation of Time is archaic English for "reconciliation", and the curve shown in the graphic has long been used to reconcile the time shown by a sundial (for example) with the local time on a clock.
But there's another complication. My wife and I live in a town in the Australian Eastern (Standard and Daylight) time zone. Clock time is the same everywhere in that zone, even though the sun rises earlier at the eastern end of the zone than it does at the western end. We're at 146°E longitude, and the standard meridian for the zone is 150°E. The 4° difference corresponds to about a quarter of an hour difference as the sun goes, which means that our Equation of Time runs about a quarter of an hour late (see above graphic again, "146°E" curve). Solar noon in our town wobbles between about half an hour later than clock noon, and just a minute earlier than clock noon.
In the first graphic above I've "corrected" the sunrise and sunset times for the Equation of Time effect. The two adjusted curves look more like what we'd expect. The longest day is clearly around 21 December, after which sunrise time gets steadily later and sunset time gets steadily earlier. What my wife had noticed was the effect the Equation of Time was having on clock times for sunset: lifting the sunset curve and almost flattening it. For the same reason, sunrise time on the clock was becoming later each day at a surprisingly quick pace.
The Earth turns 360° in 24 hours, or 15° per hour, or 1° in 4 minutes. The 4° between our town and our time zone's standard meridian means the sun rises and sets 16 minutes later here than it does at 150°E.
I think about the Equation of Time displacement this way: there are 4 days each year when solar noon equals clock noon. These are the days when the "150°E" curve crosses the "0" line in the second graphic, above. At solar noon on such a day at 150°E, the sun is at its highest point in the sky and the time is 12 noon (Australian Eastern Standard Time). It's also 12 noon at 146°E in my town, because my town is in the same time zone. The Earth continues to turn, and 16 minutes later the sun as seen from my town is at the highest point of its arc, and the time is 12.16 pm.
The data graphics were built with Gnumeric.
Last update: 2021-02-17
The blog posts on this website are licensed under a
Creative Commons Attribution-NonCommercial 4.0 International License